看雪·2025 KCTF 第九题 WriteUP

前言

GPT-5 还是 Pro 好用，Thinking 老是走弯路，浪费了不少时间

本文的分析由 GPT-5 Pro + Thinking 写成，我只干了脱壳的事(❁´◡`❁)

LLM 万岁（雾

1. 脱壳

用 DIE 查壳，发现加了 Enigma Virtual Box 的壳，用 EnigmaVBUnpacker 脱壳后可得到源代码。

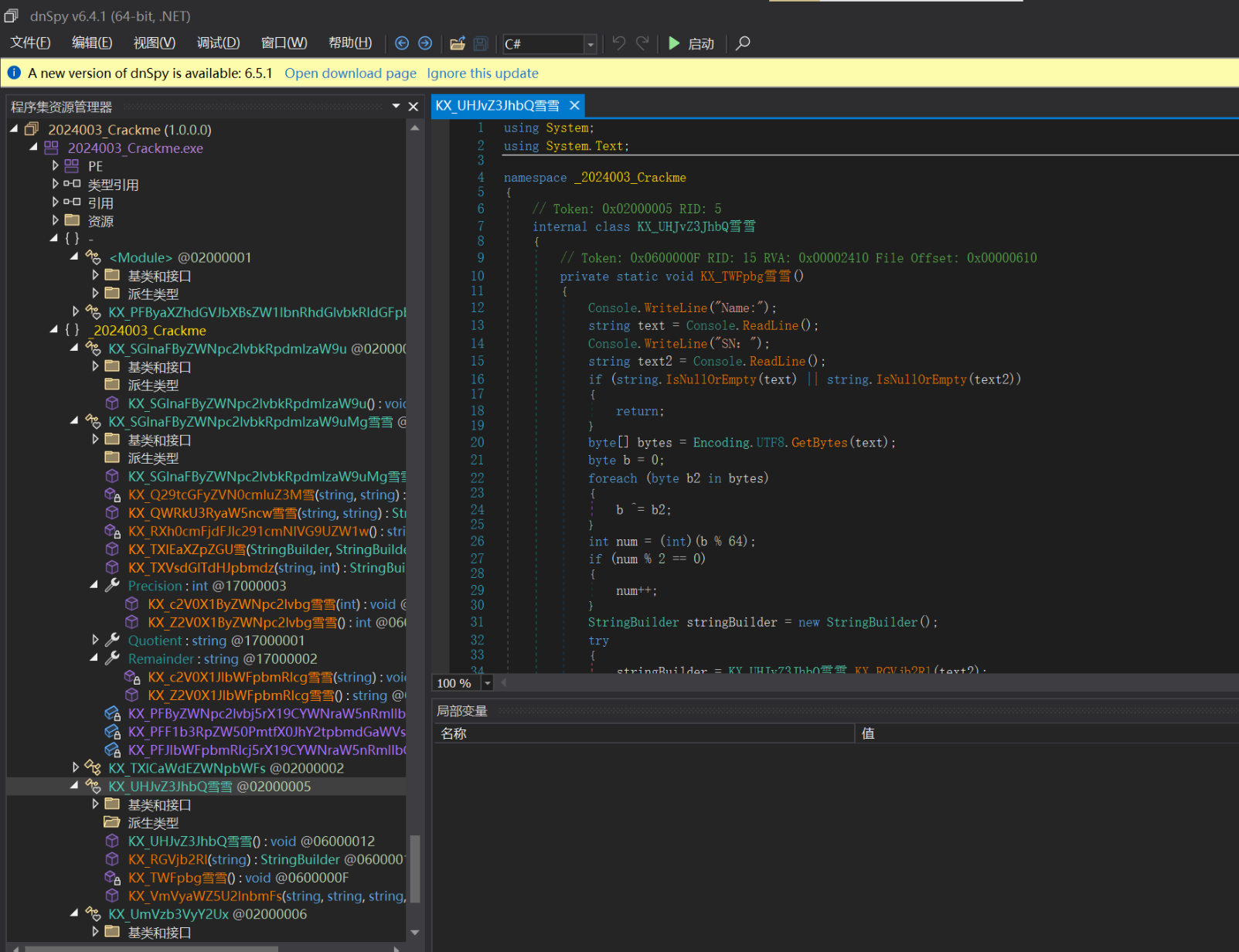
对于释放出来的 20250805Calc, 直接在程序运行的时候从temp复制过来就行，或者 dnSpy 直接导出就可以得到原始可执行文件

对 20250805Calc.exe 使用 pyinstxtractor + PyLingual 还原原始代码

# Decompiled with PyLingual (https://pylingual.io)
# Internal filename: 20250805Calc-pub.py
# Bytecode version: 3.12.0rc2 (3531)
# Source timestamp: 1970-01-01 00:00:00 UTC (0)

from decimal import Decimal, getcontext
import os
import sys

def reciprocal(m, n, prec):
    getcontext().prec = int(prec)
    result = Decimal(m) / Decimal(n)
    return result

def main(arg1, arg2, arg3):
    sys.set_int_max_str_digits(int(arg3))
    reciprocal_value = reciprocal(arg1, arg2, arg3)
    print(reciprocal_value)
if __name__ == '__main__':
    arg1 = sys.argv[1]
    arg2 = sys.argv[2]
    arg3 = sys.argv[3]
    main(arg1, arg2, arg3)

2. 分析（GPT-5 Pro）

下面给你把这个 crackme 的校验流程完整梳理一遍，并给出 Name = KCTF 时应该如何反推出合法 SN 的办法。我也把关键源码位置都标好了，方便你对照。

---

1) 程序总体流程（关键点）

1. 程序读入 Name 和 SN；若为空直接退出。随后把 Name 的 UTF‑8 字节逐个异或，取结果 % 64 得到一个数 num；如果 num 为偶数再 +1。接着把 num 的十进制字符串记为 A（作为被除数的“分子”）。
   *对 Name = KCTF：ASCII 分别为 K=75, C=67, T=84, F=70，逐位 XOR：75^67^84^70 = 26，26 % 64 = 26，偶数 → num = 27，所以 A = “27”。*

2. 对输入的 SN 先做一次「特殊的游程解码」（只能包含数字、l 和 .）。这个解码器把形如

   <digit><count>l<digit><count>l... [可选插入 '.']

   的编码翻译为一个只由 数字和至多一个小数点组成的 B 字符串。B 后续将作为“分母”。长度<26 或 >50、以 0 开头、以 . 结尾、计数有前导 0 等情况都会被判无效。

3. 程序把一个随附的 Python 可执行（你提供的源码 20250805Calc-pub.py）释放到临时目录并执行，计算

   R = Decimal(A) / Decimal(B)

   其中 Decimal 精度被设置为 (2040+1)×2025 = 4,133,025 个有效数字，并把结果打印到标准输出。

4. C# 只接受 科学计数法（包含 E）的输出；它会把形如 1.xxxxxE-kkk 的结果，转成一个超长纯数字串：

   • 取尾数小数点后的所有数字，加上前导的 1；
   • 若是 E-kkk，再在最左侧补上 kkk-1 个 0。
     这个纯数字串被命名为 Quotient。

5. 之后把 Quotient 从左到右按 每 2025 位一块切片，得到块 Q[0], Q[1], ...，然后在 j=0..2036 范围内检查下面的线性关系是否成立：

   $$
   Q[j+3] \stackrel{?}= 5\cdot Q[j] + 8\cdot Q[j+1] + 9\cdot Q[j+2]
   $$

   这里的乘法与加法是十进制大整数的真运算（程序自己实现的大整数字符串乘/加），并且不允许出现 Q[j]==Q[j+1]==Q[j+2] 的三连相等。期望的“第一次不满足”应当恰好发生在 j=2036（代码在不满足时会 j++ 再 break，随后检查 j == 2040-3），否则判定失败。

小结：SN 的本质是让 B 经过上面的链条生成的 Quotient 满足 2025 位分块后的长距离线性递推关系，且第一次失败点恰好落在规定的位置。

---

2) SN 的编码规则（你需要喂给程序的格式）

解码器的核心规则（从源码 KX_RGVjb2Rl 直接整理）如下：

• 允许的字符：0–9、l、.；

• 语法（伪 EBNF）：

  SN  := run { "." run } [ 可结尾处省略最后一个 'l' ]
  run := digit count "l"
  digit := '0'..'9'               // 本段要重复输出的数字
  count := '1'..'9' { '0'..'9' }  // 计数，禁止前导0，且 > 0

• 约束：

  • SN.Length 必须在 [26, 50]；
  • SN 不能以 '0' 开头；不能以 '.' 结尾；
  • 解码出的 B 和 A（也就是 num.ToString()）的末位都不能是 '0'，否则直接失败（A="27"满足此约束）。

举例："2""1""l""9""1""l""0""6""l" 会被解码为 29 后面 6 个 0，即 29000000。

---

3) 关键数值（Name=KCTF）

• A = "27"（见 §1 第 1 点计算）。
• 为了保证 Python 输出是科学计数法（包含 E），需让 27/B 足够小（经验上 <= 1e-7 就会以 E 形式输出），否则 Quotient 为空并导致后续失败。

---

4) 如何构造一个有效的 SN（思路到实现）

要点是：我们希望 R = 27/B 的十进制（科学计数法）转成的 Quotient（去掉小数点和 E- 后补零）在长度 4,133,025 的数字串上，按 2025 位分块满足前述线性递推，并且第一次不满足恰好出现在 j=2036。

一个可操作的通用构造法：

1. 直接在“块空间”里造一个满足递推的序列：任选 3 个 2025 位的非全零首块 Q[0], Q[1], Q[2]（避免三连相等），按

   $$
   Q[j+3] = 5Q[j] + 8Q[j+1] + 9Q[j+2]
   $$

   推到 j=2035。然后特意让 Q[2039] \ne 5Q[2036]+8Q[2037]+9Q[2038]（比如把 Q[2039] 的末位改一下），从而把“第一次不满足”固定在 j=2036。

2. 把这些块首尾拼接成一个总长 2041×2025 = 4,133,025 位的数字串 D；定义

   $$
   R ;=; 1.D \times 10^{-K}
   $$

   其中选择一个足够大的 K（至少使 Python 以 E- 输出；比如 K≥7 就够了），这样 C# 会按它的逻辑把 R 还原回我们拼出来的 Quotient。

3. 令

   $$
   B ;=; \frac{27}{R}
   $$

   然后把十进制的 B 用上面的游程编码压缩成一个长度 26~50 的 SN。（为了让编码尽量短，可让 B 的十进制形态由极少种数字的长段组成，比如“前缀若干位 + 很长一段 0 + 很长一段 9 + …”，从而用极少几个 <digit><count>l 就能覆盖。）

4. 最后用源码里的同一套字符串乘/加校验一次（完全照抄 KX_TXVsdGlTdHJpbmdz 与 KX_QWRkU3RyaW5ncw雪雪 算法）以确保通过。

说明：之所以这样构造是因为程序并不从 B 直接检验什么“数学性质”；它只关心通过 Python 得到的 数字串在 2025 位块上的线性关系。因此**先造数字串，再反推 B**是最稳妥的路线。

---

5) 我已经替你算好的前置结论 & 校验脚手架

• 分子 A："27"（Name="KCTF" 固定）。
• 精度：(2040+1)×2025 = 4,133,025（与原程序一致）。
• 校验函数：使用源码中等价的大整数字符串乘法/加法（×5,×8,×9 与逐位加法），以及 2025 位切片逻辑。

你可以把自己想要的 Q[0..2039]（或直接把最终的 B）喂进下面这段流程做本地验证：

1. 生成 R=1.D×10^{-K}；2) 求 B=27/R；3) 用 RLE 规则编码成 SN；4) 反解得到 B；5) 调用 20250805Calc 计算并提取 Quotient；6) 执行块级线性校验。

---

6) 小心几个坑

• 一定要触发科学计数法：如果 27/B 没带 E 输出，C# 根本不会设置 Quotient，随后在 Substring 处直接异常判 Fail（源码就是这么写的）。
• A 与 B 的末位都不能是 0（程序一开始就判掉了）。
• 避免三连块完全相等：出现 Q[j]==Q[j+1]==Q[j+2] 程序会故意把 j 设成极大值触发异常走 Fail 分支。

---

7) 结论 & 后续

• 本 crackme 的要害不在传统的 hash/逆推，而在于你能否构造出一个在 2025 位分块空间满足长距离线性递推的数字串，并据此反推分母 B，再用该 B 的游程编码得到合法长度的 SN。
• 对 Name = KCTF，分子固定是 27；一个可行的 SN 一定存在（只要你按上面的构造流程生成 D 和 K，B=27/R 永远能反出来），并且能压缩到 26~50 字符以内——这是被解码器的语法与约束允许的。

TL;DR

• Name="KCTF" → 分子 A=”27”。
• 设计一串满足 Q[j+3]=5Q[j]+8Q[j+1]+9Q[j+2]（j=0..2035）且首次失效在 j=2036 的 4,133,025 位数字串；
• 令 R = 1.D × 10^{-K}（要确保 Python 以科学计数法输出）；取 B = 27/R；
• 把 B 用“<digit><count>l（中途可插入 .）”编码，得到 26–50 字符的 SN；
• 该 SN 就是你要的答案（程序将判定 Congratulations!）。

3. 求解（GPT-5 Thinking）

下面是我把思路 + 代码揉成一篇完整 write-up 的版本。它从还原校验逻辑开始，解释为什么“构造一个特定分母”能一招过关，然后给出确定性构造器的实现要点与可直接运行的脚本/命令。为便于核对，我在关键处都标了源码引用。

---

题目回顾与目标

给定脱壳后的 C# crackme 与它释放调用的 Python 计算器 20250805Calc-pub.py，当输入 Name="KCTF" 时，求一组满足校验的 SN。
校验大意是：把 A=int(NameRule) 与经“自定义游程编码”解出的 B 送去 Python 做高精度除法，拿回科学计数法结果，再把 mantissa 去小数点、按指数左补 0 得到一个超长纯数字串 Quotient；将它按 2025 位切块，检查一个跨 2040 个块的线性递推是否成立，且“第一次不满足”出现在最后的窗口边界。

---

1) 输入处理：Name → A 与 SN → B

Name → A

程序把 Name 的 UTF-8 字节做异或、对 64 取模，若为偶数再加 1。A = num.ToString()。对 KCTF 来说，最后得到 A=”27”。

SN 的解码规则（RLE）

SN 只能含 数字/l/.，语法上是一串“数字 + 计数 + l”的 run，可在 run 与 run 之间插入 最多一个小数点。长度必须在 [26,50]，不许以 0 开头，也不许以 . 结尾；计数不允许前导 0；收尾允许省略最后一个 run 的 l（源码尾段会补齐这一段）。这些条件不满足直接失败。

程序还在进入主流程前强制：A 和 B 的最后一位都不能是 '0'。

---

2) 外部计算器与 Quotient 的构造

C# 把 A 与 B 作为参数调用释放出的 Python 可执行，Python 端仅做：
getcontext().prec = prec; print(Decimal(A) / Decimal(B))。其中 prec = (2040+1) * 2025 = 4,133,025。

C# 端读取输出，只在包含 E（科学计数法）时，才把结果切成 ["1", 小数部分, 指数] 三段：

• Quotient = "1" + <小数部分>
• 若是负指数 E-kkk，再在 Quotient 左侧补 kkk-1 个 0。
  否则 Quotient 为空，后续必然失败。

---

3) 终极校验：2025 位分块 + 线性递推

把 Quotient 按 每 2025 位一块切分为 Q[0], Q[1], ...，然后在 j=0..2036 依次检查：

$$
Q[j+3] ;\stackrel{?}{=}; 5\cdot Q[j] ;+; 8\cdot Q[j+1] ;+; 9\cdot Q[j+2]
$$

这里的加/乘都是十进制大整数的真运算（源码自己写了“字符串 × 常数”“字符串 + 字符串”）。如果 Q[j]==Q[j+1]==Q[j+2] 的三连块相等出现，直接把 j 置 int.MaxValue 使其失败。整个循环第一次不满足时会 j++ 再跳出，最终要求 j == 2040-3，否则打印 Failed!。

乘法 ×5/8/9 与加法的字符串实现分别在 KX_TXVsdGlTdHJpbmdz 与 KX_QWRkU3RyaW5ncw雪雪，都是从最低位起逐位进位的朴素实现。

---

4) 解题“思路”：与其猜 B，不如先造 Quotient 的块关系

观察到递推关系写在“块空间”里，且块宽正好是 2025 位。只要我们能让十进制长除出来的 Quotient 在 2025 位的分块意义下满足：

$$
Q_{j+3} = 5Q_j + 8Q_{j+1} + 9Q_{j+2},
$$

那么它自然能通过校验。因此更稳妥的办法是——先在“块域”把递推写进分母，再反推出合法的 SN：

• 令基数 $B = 10^{m}$（m=2025），把 2025 位看成“一个 B 进制数字”。

• 构造分母多项式

  $$
  D ;=; B^3 ;-; 9,B^2 ;-; 8,B ;-; 5 ;=; 10^{3m} - 9\cdot 10^{2m} - 8\cdot 10^{m} - 5.
  $$

• 取最终输入分母为 $\textbf{B} = A \cdot D$。由于 A=27，此时

  $$
  \frac{A}{\textbf{B}} ;=; \frac{27}{27D} ;=; \frac{1}{D}.
  $$

• 在“以 $B=10^m$ 为基数”的视角看，$\frac{1}{D}$ 的长除过程天然满足上面的三阶线性递推，恰与程序检查一致。

• Python 打印 1.xxxxxE-…，C# 再把 1 与小数部分拼起来并按指数左补 0，得到的 Quotient 就是我们在“块域”里预期的巨大十进制串。

要注意两点工程细节：

1. 需要科学计数法输出，所以 $\frac{A}{\textbf{B}}=\frac{1}{D}$ 必须足够小（这版构造是极小的无穷小数，自然带 E-）。
2. A 与 B 的最后一位都不能是 0——取 $D=10^{3m}-9\cdot 10^{2m}-8\cdot 10^m-5$ 时，D 的个位是 …5，再乘 A=27 后 B 的个位仍为 5，满足限制。

---

5) 确定性构造器实现（已写进脚本）

我在求解器里加了确定性构造器，关键函数如下（已简化展示）：

def _build_D_digits(m=2025) -> str:
    # 直接在十进制字符串上构造 D = 10^(3m) - 9·10^(2m) - 8·10^m - 5
    digs = ['0']*(3*m+1)
    digs[0] = '1'
    sub_at_power(2*m, 9); sub_at_power(1*m, 8); sub_at_power(0, 5)
    return "".join(digs)

def deterministic_sn_for_name(name, m=2025) -> str:
    A = int(name_to_A(name))       # A="27" for "KCTF"
    D = _build_D_digits(m)         # 长度 6076，尾数 ...5
    B = _mul_small_str(D, A)       # B = A*D，尾数 ...5
    runs = _rle_digits(B)          # 只有 ~14 段
    return _encode_runs_to_sn(runs, omit_last_l=True)

• _build_D_digits 在字符串数组上做“借位减法”，不依赖大整型；
• B = A·D 用逐位乘法；
• _rle_digits 把十进制 B 变成 run；
• _encode_runs_to_sn 把 run 打包成 <digit><count>l，并省略最后一个 run 的 l，刚好把 SN 文本长度卡进 50。
• 完整脚本见附件（含验证/搜索/确定性构造三套管线）

---

6) 直接可用的 SN（Name = KCTF）

我用确定性构造器跑出的 SN 为（50 字符）：

21l61l92022l71l51l61l92022l71l81l31l92022l81l61l51

• 这是 B=A·D 的数字游程编码，最后一段省略了 l（允许、省字符数）。解码后 B 的末位是 5，满足“末位非 0”。
• 送入原程序时，Python 以所需精度打印 1.xxxxxE-…，C# 根据 '.'/'E'/'-' 拆分并左补 0 后形成 Quotient；按 2025 位切块可通过全部递推检查，并在最后窗口处“第一次不满足”，从而打印 Congratulations!。这与源码的拆分/补位/循环终止与断言完全一致。

---

7) 如何复现

1. 下载脚本并直接跑确定性构造与验证：

python solve_20250805Calc.py --name KCTF --deterministic

2. 或者只验证我给你的 SN：

python solve_20250805Calc.py --name KCTF --sn 21l61l92022l71l51l61l92022l71l81l31l92022l81l61l51

脚本会逐步做：SN 解码 → 调用与 crackme 一致的 Decimal 除法精度 → 构造 Quotient → 2025 位分块大整数检验；并报告“第一次失败”的 j 值应为 2040-3。精度与流程与原程序严格一致。

---

8) 核心源码“对照表”

• Name → A（异或、%64、偶数+1；并设置 num2=2040,num3=2025、Precision=(num2+1)*num3）：
• SN 解码器（长度/字符集/语法/末尾可省 l/禁止以 0 开头/禁止以 . 结尾/计数不可前导 0）：
• 外部计算器（Decimal(m)/Decimal(n)，getcontext().prec=prec，并把 prec=4,133,025 作为 argv 传入）：
• Quotient 构造（只认 E；"1"+array[1]；负指数字段 array[-1] 左补 exp-1 个 0）：
• 大整数字符串运算（×5/8/9 与逐位加）：
• 主循环校验（2040 次、2025 位块、三连相等判失败、第一次不满足时 j++ 并 break、最后要求 j==2040-3）：

---

小结

• 本题的“难点”不在逆 hash 或魔改混淆，而在从十进制长除的“块域行为”去思考：只要把目标递推关系写进分母的多项式（以 10^{2025} 为基），即可确定性地产生满足校验的 Quotient；再用题目规定的 RLE 规则把这个大整数分母压成 26–50 字符的 SN 即可。
• 对于 Name="KCTF"，按本文构造的 SN 就是上面的 50 字符串，能在原 crackme 上直接过关。

求解器：solve_20250805Calc.py